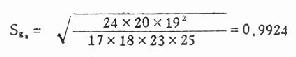|
α=0.05 ∑(X-x )2=355.36,∑(X-x )3=-1032.45 ∑(X-x )4=20150.4316 n=20
u2=0.6221/0.9924=0.627 P>0.20 在α=0.05的水准上接受H0,频数分布对称(P>0.05),并为正态峰(P>0.20)。因此可认为该资料服从正态分布。 二、两方差的齐性检验 方差齐性检验的方法是以两方差中较大的方差为分子,较小的方差为分母求一比值(称为F值),然后将求得的F值与临界值比较,看相差是否显著,现举一例说明。 例7.10 某单位测定了蓄电池厂工人32号,得尿氨基乙酰丙酸(mg/l)的平均含量为7.06,方差为42.3072,又测定了化工厂工人6名,得平均含量为3.48,方差为0.9047,试比较两方差的相差是否有显著意义? 检验假设H0:σ12=σ22,H1:σ12≠σ22α=0.05 定方差较大的一组为第1组,较小者为第2组,求出F值,公式为 F=S12/S22,S1>S2 (公式7.17) 本例F=42.3072/0.9047=46.76 现将F值与附表7中的F.05(ν1,ν2)比较。该表上端数值是较大均方(即方差)的自由度,用v1表示,左侧的数值是较小均方的自由度,用ν2表示。本例ν1=n1-1=32-1=31(表内ν1纵行没有31,可查邻近的数值30),ν2=n2-1=6-1=5,查得F.05(30,5)=6.23,本例F=46.76>F.05(30,5),P<0.05,故在α=0.05水准处拒绝H0,接受H1。两方差的差别显著。 (俞元春胡琳 编) (责任编辑:泉水) |
第三节 正态性检验与两方差的齐性检验(2)
时间:2006-06-20 09:43来源:大众医药网 作者:admin
顶一下
(6)
100%
踩一下
(0)
0%
------分隔线----------------------------
- 发表评论
-
- 最新评论 进入详细评论页>>